第一章：1.2 直角三角形 课时二

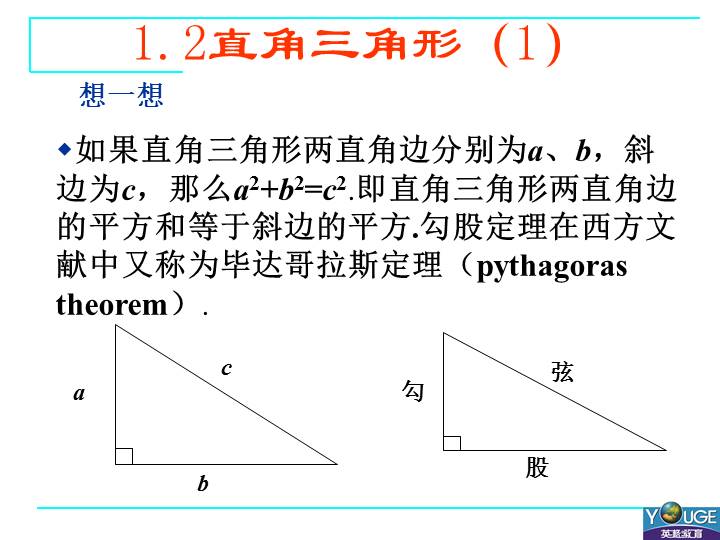
如果直角三角形两直角边分别为a、b，斜边为c，那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理（pythagoras theorem）.
想一想 1.2直角三角形（1）

方法一: 拼图计算 方法二：割补法 方法三：赵爽的弦图 方法四：总统证法 方法五：青朱出入图 方法六：折纸法 方法七：拼图计算
这些证法你还能记得多少?你最喜欢哪种证法?
勾股定理的证明
这个证明方法出自一位总统, 1881年，伽菲尔德(J.A. Garfield )就任美国第二十任总统,在 1876 , 利用了梯形面积公式. 图中三个三角形面积的和是 2×ab/2＋c/2;梯形面积为(a+b)(a+b)/2; 比较可得:c2 = a2+b2 .
伽菲尔德的证法在数学史上被传为佳话,后来，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统”证法．
勾股定理的证明
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
已知:如图(1),在△ABC中,AC2+BC2=AB2. 求证:△ABC是直角三角形.
勾股定理逆定理
证明:作Rt △A′B′C′使∠C′ =900,A′C′=AC,B′C′=BC(如图),则
已知:如图(1),在△ABC中,AC2+BC2=AB2. 求证:△ABC是直角三角形.
A′C′2+B′C′2=A′B′2(勾股定理).
∵AC2+BC2=AB2(已知), A′C′=AC,B′C′=BC(作图),
∴ AB2=A′B′2(等式性质).
∴ AB=A′B′(等式性质).
∴ △ABC≌ △A′B′C′(SSS).
∴ ∠A=∠A′＝ 900(全等三角形的对应边).
∴ △ABC是直角三角形(直角三角形意义).
逆定理的证明
′ 勾股定理的逆定理 如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
这是判定直角三角形的根据之一.
在△ABC中 ∵AC2+BC2=AB2(已知), ∴△ABC是直角三角形(如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形).
勾股定理逆定理
直角三角形两直角边的平方和等于斜边的平方.
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
观察上面两个命题,它们的条件与结论之间有怎样的关系?与同伴交流.
再观察下面两组命题:
如如果两个角是对顶角,那么它们相等, 如如果两个角相等,那么它们是对顶角如;
如果小明患了肺炎,那么他一定会发烧, 如果小明发烧,那么他一定患了肺炎;
上面每组中两个命题的条件和结论之间也有类似的关系吗?与同伴进行交流.
命题与逆命题
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
你能写出命题“如果两个有理数相等, 那么它们的平方相等”的逆命题吗?
它们都是真命题吗? 想一想:一个命题是真命题,它逆命题是真命题还是假命题?
命题与逆命题
一个命题是真命题,它逆命题却不一定是真命题.
我们已经学习了一些互逆的定理,如: 勾股定理及其逆定理, 两直线平行,内错角相等;内错角相等,两直线平行.
你还能举出一些例子吗?
想一想: 互逆命题与互逆定理有何关系?
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
定理与逆定理
如图(单位：英尺),在一个长方体的房间里,一只蜘蛛在一面墙的正中间离天花板1英尺的A处,苍蝇则在对面墙的正中间离地板1英尺的B处. 试问:蜘蛛为了捕获苍蝇,需要爬行的最短距离是多少?
动手试一试
勾股定理: 如果直角三角形两直角边分别为a、b，斜边为c，那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理（pythagoras theorem）. 勾股定理的逆定理: 如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
本课小结
命题与逆命题 在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题. 定理与逆定理 如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
本课小结
1.如图，在△ABC中，已知AB=13cm, BC=10cm,BC边上的中线AD=12cm. 求证:AB=AC.
证明:∵BD=CD,BC=10cm(已知),
∴ BD=5cm(等式性质).
∵ AD2+BD2=122+52＝144+25=169, AB2=132=169,
∴AD2+BD2=AB2.
D ∴ 在△ABD中,
∴△ABC是直角三角形(如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形).
在Rt△ADC中 ∴AC2=DC2+AD2=122+52＝144+25=169,
∴AC2=AB2. ∴AB=AC(等式性质).
动手试一试
2.房梁的一部分如图所示,其中BC⊥AC,∠A=300,AB=10m,CB1⊥AB, B1C1⊥AC,垂足为B1,C1,那么BC的长是多少？B1C1呢？
解:∵BC⊥AC,∠A=300,AB=10m(已知),
∴ BC=AB/2=10÷2＝5(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半),
又∵CB1⊥AB,∠BCB1=900-600=300(直角三角形两锐角互余),
∴CB1=BC/2=5÷2＝2.5(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).
∴AB1=AB-BB1=10-2.5=7.5(等式性质).
动手试一试
动手试一试 ∴B1C1=AB1/2=7.5÷2＝3.75(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).
3.如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少？

解:如下图,将四棱柱的侧面展开,连结AC1,
∵AC=10cm,CC1=8cm(已知),
老师提示:对于空间图形需要动手操作,将其转化为平面图形来解决.
答:蚂蚁需要爬行的最短路径是 cm.
动手试一试
课后习题